Jottings on Celestial and Great Circle Navigation
In response to a network news item I posted, several people asked for
a simple explanation of navigation. What follows is my reply.
Shape of the Earth
The shape of the earth is irregular, being more like a
pear (thicker at the top) than a
sphere. For the purposes of measurement, an imaginary surface called
the 'geoid' is used. This surface is the level to which the oceans would
settle when the forces of gravity and centrifugal forces of rotation are
taken into account. It is rarely used for navigation, but surveyors and people
who write code for satellite navigation and mapping systems need to use this
model. A reasonable approximation for navigation purposes is to model
the earth as an oblate spheroid. The spheroid
is usually specified as a semimajor axis and a flattening factor. From
these values the semiminor axis and eccentricity can be calculated.
These values are formalised in the "World Geodesic System" and the current
values are :-
WGS 1984
a = 6378137 metres (semimajor axis)
1
f = _____________ (flattening factor)
298.257223563
a - b
= _____ (where b is semiminor axis)
a
e^2 = 2f - f^2 (eccentricity)
Unless you require absolute accuracy (surveys, satellite mapping), most
calculations of great circle distances use straight spherical geometry. For
short distances (less than 600 nautical miles (NM)), distances are
calculated using meridional parts either from tables or with a
computer program
(and brief documentation).
A rhumb line
is a straight line on a Mercator map projection. It intersects all the
parallels of latitude at a constant angle. Except for courses that are
East/West along the equator
or North/South (which would be great circles), these lines
would be a spiral on the earth's surface (a loxodrome). A great circle
track would be a curve on a Mercator projection and a straight line
on a Gnomonic projection (usually only used for high latitudes).
Mercator Projection
Gnomonic Projection
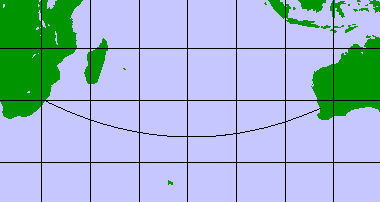
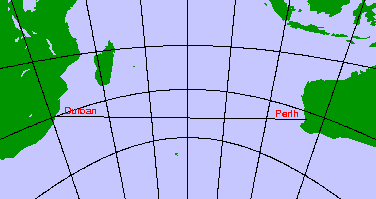
For navigation, great circles are only worth while for long.... passages.
If you left Durban (South Africa) and sailed/flew to Perth (Australia),
the great circle distance is 4244 nautical miles, while the rumb distance
is 4376, a saving of 132 nautical miles.
The compass heading that must be steered to achieve a
great circle
changes continuously throughout the voyage. It is usual practice
to break the voyage into segments and calculate the rhumb approximation
for each segment. If you are sailing you could make greater gains in speed
by taking advantage of known currents and winds rather than using a great
circle track.
Celestial Navigation
Many people make the mistake of thinking that is is possible to calculate
your position at any time using sun/star fixes.
Except for a few special cases, it is only possible to use stars to make
a direct fix when both the stars and the horizon are visible ie just before
sunrise and just after sunset. During the day the sun is available but
a single sight can only give a line of position on a map, not your exact
position. A second sun sight taken some hours latter is required to get two
intersecting lines (the earlier line is 'run on' to account for
the change in position; commonly called a sun-run-sun).
If the moon or a planet is available then is possible
to take them in conjunction with the sun and establish an observed position.
The data required to make a position fix are as follows :-
-
Accurate knowledge of the time, either GMT (UTC) or local time and
time zone. An error of four seconds is equal to
one nautical mile at the equator.
-
An accurate measurement of the altitude (angle to the horizon)
of the body (sun. moon, planet or star).
One minute of arc error is equal to one nautical mile. This
measurement has to be corrected for height of eye, dip of
the horizon, refraction of the atmosphere and possibly
parallax (moon and some planets) and unusual temperatures or
pressures.
-
The declination of the body from tables of ephemerals like a
nautical almanac, air navigation tables or a computer program.
-
An estimate of your position.
Sight Reduction
The taking of a sight and the calculation using that data
is called 'sight reduction'.
For a single sight, the result is a bearing and distance from your estimated
position to a line that you are on (called a line of position). You could be
at any position along the line. A second sight taken of another object at least
40 degrees away from the first will give a second line of position. Where the
two intersect is your observed position. Taking a third sight will give
another line, though they will probably not all intersect at the same point.
You will probably get a small triangle (or cocked hat).
At sunrise/sunset you can probably take several sights of stars in the available
time (about 20 minutes depending of latitude). During the day you will usually
only have the sun. In this case you have to take measurements some hours apart
and plot them. If you have moved between the observations, then you have to
compensate for the movement when you plot the positions.
Meridian Passage
Meridian passage is handy since neither the time or an estimate of your
position is required (except for hemisphere). The technique is to observe
the sun (or moon) and measure its altitude when it is at its highest
point (it will always be due North or South). You will have several minutes
where the sun will appear to hover,
before it's altitude starts decreasing. Your latitude can be
calculated directly given this altitude and the declination of the
body (from the almanac).
With an accurate chronometer, it is possible to calculate longitude. You
will have to take a dozen or more sights starting about 20 minutes before
meridian passage and 20 minutes after, then plot the altitudes again time and
estimate the exact time for the meridian passage. This time can be translated
into longitude.
Prime Vertex
This is when the body is rising or setting, usually the Sun.
Due to atmospheric distortion
the Sun will be one semidiameter above the horizon when it has just
risen. The true bearing of the object can be calculated
given an estimate of your latitude. It is mainly used as a
compass check though
the time of this event can be used to calculate longitude.
Also known as a true amplitude.
Instruments
The basic instruments required for celestial navigation are
an accurate chronometer (read quartz watch) and a
sextant. A good instrument should be accurate to 0.1 minutes
of arc. It is debatable that it is possible to take sights
to this accuracy. The problem with using a sextant is that a
clear horizon must be available as a reference point. The
only accurate horizon is the sea surface, therefore the
marine sextant is
useless inland. It is possible to make an artificial horizon
using a bath of
oil or mercury to reflect the object being measured and
halving the angle obtained. There is a variant of the
sextant called a 'Bubble Sextant' that has an inbuilt level
to determine the horizon. This is only useful if the sextant is
on a stable platform and was developed mainly for use in aircraft.
Tables
The calculations required for most celestial navigation can
be done on a simple scientific calculator. Replacing the
nautical almanac is another matter. The latter provides for each
day of the year the following :-
-
The Greenwich Hour Angle (GHA) and declination for the Sun,
Moon, Planets and Aries for each hour of the
day.
-
The declination and Sidereal Hour Angle (SHA) for 57 selected
stars.
-
The times of sunrise,
sunset, moonrise, moonset and twilight for
various latitudes.
-
Meridian passage times for the sun, moon
and planets.
Supplementary tables are provided for the following:-
-
Dip and height of eye corrections.
-
Altitude corrections for the sun, stars and planets.
-
Additional altitude corrections for non-standard conditions
of temperature and air pressure.
-
Star Charts.
-
Addition data for 173 stars.
-
Tables for Polaris.
-
Sight reduction tables.
-
Conversion of arc to time.
-
Increments and corrections to GHA and declinations for minutes
and seconds after a whole hour.
Programs
As stated in the previous section, replacing the almanac
would be difficult. There have been a few programs on the
network, namely 'planets' and
xephem that will provide
declinations and right-ascensions (RA) for the sun, moon and
planets. It is fairly easy to convert RA to GHA. The rest
of the calculation for sight reduction involves making all the
corrections for the sight and solving a half haversine
equation.
Reference Books
American Practical Navigator, Bowditch
The lastest edition is a single volume of 1350 pages, last updated in 1995.
It removes a lot of the older navigation methods and tables, and updates
various sections, especially electronic navigation and the introduction
of Navstar (GPS) which the replaces Navsat (Transit) satellite system.
The older version
is a two volume set published by the US Defence Mapping Agency
Hydrographic/Topographic Center. It was first published in 1802.
Volume I (1414 pages) covers fundamentals, plotting and dead reckoning,
celestial navigation, the practice of navigation, navigational safety,
oceanography, weather and electronics (satellite, Omega, Loran and other
hyperbolic systems). All for the princely sum of $45 from Boat Books in
Sydney.
Volume II (961 pages) has useful tables, mathematics for navigation,
and navigational calculations. It is a good source of information for
the formulae that are used to generate the various tables.
Nories Nautical Tables
This is a book of tables for use in navigation, not much theory. 570 pages.
Nautical Almanac
The ephemerals are published each year. The yachtsman's edition is $20 or so.
All maps and projections generated by the
GMT (Generic Mapping Tools) package, see
www.soest.hawaii.edu/gmt.
Copyright Notice



